Tag Archive for: differential equations

The Role of Differential Equations in Enhancing AI Predictive Models

Solving Differential Equations: The Backbone of Predictive Models in AI

As someone deeply entrenched in the world of Artificial Intelligence (AI) and machine learning, I’ve found differential equations to be a powerful tool in predicting and understanding behaviors in complex systems. These equations, which involve functions and their derivatives, are fundamental in describing various phenomena in physics, engineering, and now, prominently, in AI.

Understanding Differential Equations

Differential equations can be broadly classified into two types: ordinary differential equations (ODEs), which involve a single variable and its derivatives, and partial differential equations (PDEs), which involve multiple variables and their partial derivatives. For the scope of this discussion, our focus will center on ODEs and their application in AI, particularly in process automation and forecasting models.

The Math Behind ODEs

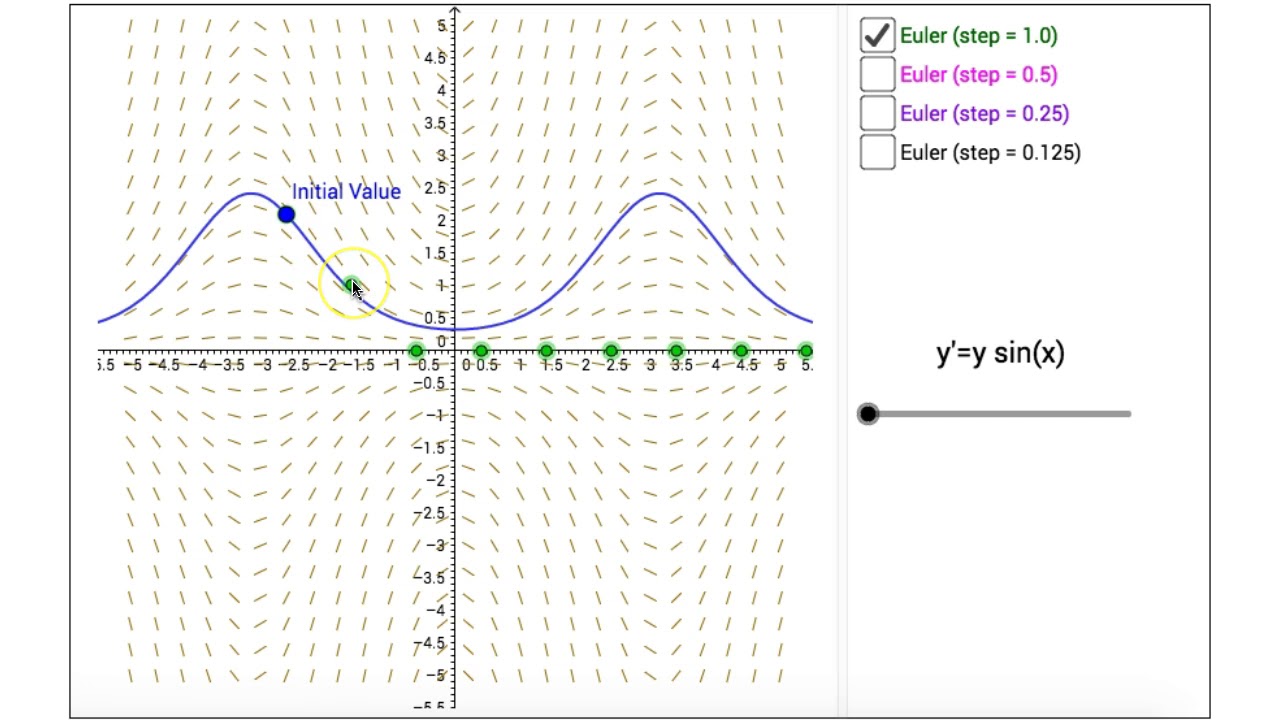
At its core, an ODE is an equation that contains a function of one independent variable and its derivatives. The goal is to find the function that solves the equation. An ODE is generally represented as:

\( \frac{dy}{dx} = f(x, y) \)

Where \( \frac{dy}{dx} \) represents the derivative of \(y\) with respect to \(x\), and \(f(x, y)\) is a given function. The solution to an ODE is the function \( y = f(x) \) that satisfies this equation for a given initial condition \( y(x_0) = y_0 \).

Application in AI and Machine Learning

In AI, particularly in the development of machine learning models, ODEs are pivotal in defining the way a system changes over time. For instance, in process automation, understanding and predicting the time evolution of a system enables the design of more efficient algorithms.

To put it into perspective, consider the training of a neural network. The adjustment of weights in the network during training can be described by a differential equation, where the derivative of the loss function with respect to the weights dictates the direction and magnitude of the weight adjustment. This is a fundamental aspect of gradient descent, a widely used optimization method in machine learning.

Case Study: Forecasting with AI

Consider the problem of predicting stock prices. This is a complex system influenced by myriad factors, but at its heart, it can be modeled using differential equations. By analyzing historical data, we can establish a differential equation that describes how the stock price changes over time. The solution to this equation gives us a function that can forecast future prices under given conditions.

Illustrating the Process

  • Identify key variables that influence stock prices (e.g., market demand, interest rates).
  • Derive a differential equation that describes the relationship between these variables and the stock price.
  • Solve the differential equation using appropriate numerical methods, given initial conditions derived from historical data.
  • Use the solution to predict future stock prices.

Challenges and Opportunities

Solving differential equations, especially non-linear ones, can be computationally intensive. However, advancements in computational methods and hardware have made it possible to tackle increasingly complex equations, opening new avenues for AI applications. This intersection between mathematics and computer science not only enables us to solve old problems more efficiently but also to explore new problems that were previously beyond our reach.

<Advanced computational methods>

Conclusion

The interplay between mathematics, particularly differential equations, and AI is a testament to the multidisciplinary nature of solving complex problems. As we continue to push the boundaries of what’s possible with AI, the foundational role of differential equations in understanding and predicting the behavior of complex systems remains undiminished. For enthusiasts and professionals alike, the journey through this mathematical landscape is both challenging and rewarding, offering insights that are crucial for advancements in AI and beyond.

<The interplay between math and AI>

/0 Comments/by

Harnessing Numerical Methods for Superior AI Predictive Models

“`html

The Elegance of Numerical Methods in AI Predictive Models

In the realm of Artificial Intelligence and Machine Learning, precision and accuracy are paramount. It’s here that numerical analysis not only finds its application but also shines, bridging the gap between theoretical models and real-world data. As a consultant specializing in AI, I’ve witnessed firsthand the transformative power of numerical methods in predictive modeling.

Understanding Numerical Analysis

Numerical analysis is a branch of mathematics that devises, analyzes, and implements algorithms for obtaining numerical solutions to problems inherent in continuous mathematics. This discipline is the backbone of computational models, especially in areas requiring the solution of complex equations that are difficult or impossible to solve analytically.

Case Study: Solving Differential Equations

One of the most compelling examples of numerical analysis in action is in solving differential equations for predictive models. Differential equations are vital in modeling real-world processes in physics, engineering, and notably, in AI predictive models. The Role of Differential Equations in Enhancing AI Predictive Models further elucidates their importance.

Numerical Methods for Differential Equations

There are several numerical methods available for solving differential equations, such as Euler’s method, the Runge-Kutta methods, and the finite element method. Each has its advantages and specific use cases, but all serve the purpose of approximating solutions to otherwise intractable models.

Euler's method visualization

Let’s delve a bit deeper into Euler’s method, a fundamental numerical approach for solving ordinary differential equations (ODEs). It proceeds as follows:

  • Given an initial value problem \(y’=f(t,y), y(t_0)=y_0\),
  • Euler’s method approximates y at subsequent points by \(y_{n+1} = y_n + h*f(t_n, y_n)\),
  • where \(h\) is the step size and \(t_{n+1} = t_n + h\).

Although simple, Euler’s method lays the foundation for more complex algorithms and illustrates the fundamental idea of progressing step-wise to approximate solutions over a range.

Applying Numerical Methods in AI

My experience at DBGM Consulting, Inc., particularly in developing machine learning models for self-driving robots, highlighted the indispensability of numerical methods. For instance, optimizing pathfinding algorithms or sensor data interpretations invariably resorts to solving differential equations, for which numerical analysis provides the tools.

Pathfinding algorithm visualization

Numerical analysis, especially in AI, isn’t just about finding solutions—it’s also about ensuring these solutions are computationally feasible and aligned with real-world data. In essence, numerical methods help translate mathematical models into actionable intelligence, crucial for anything from process automation to predictive modeling.

Conclusion

The fusion of numerical analysis with AI and machine learning brings forth solutions that are both innovative and grounded in mathematical rigor. As someone who has navigated the intersection of technology, mathematics, and real-world application, I assert the value of numerical methods is immeasurable. They empower us to solve complex problems, optimize algorithms, and ultimately, drive forward the frontier of what’s possible in AI and beyond.

Machine learning model visualization


“`

/0 Comments/by
Link to: Get in touch

Let’s collaborate!

Contact Me

DAVID MAIOLO

 The content on this website, including text, photographs, and any other media, is the property of David Maiolo unless otherwise noted. No part of this website may be reproduced, distributed, or transmitted in any form or by any means, including photocopying, recording, or other electronic or mechanical methods, without the prior written permission of the owner.

DISCLAIMER

The information provided on this website is for general informational purposes only. While I strive to keep the information up-to-date and correct, I make no representations or warranties of any kind, express or implied, about the completeness, accuracy, reliability, suitability, or availability with respect to the website or the information, products, services, or related graphics contained on the website for any purpose. Any reliance you place on such information is therefore strictly at your own risk. In no event will I be liable for any loss or damage including without limitation, indirect or consequential loss or damage, or any loss or damage whatsoever arising from loss of data or profits arising out of, or in connection with, the use of this website. *This website may include links to other websites which are not under the control of David Maiolo. I have no control over the nature, content, and availability of those sites.

© 2024 David Maiolo