Tag Archive for: general relativity

Understanding Gravitational Memory Effects: A New Frontier in Cosmic Exploration

The Immense Power of Gravitational Memory and Its Potential Insights

When we think about the universe, we often consider vast distances, colossal cosmic events, and an ever-expansive timeline reaching back billions of years. One of the most fascinating phenomena is that space itself can “remember” certain events, a concept known as gravitational memory. This not only excites physicists like myself, but also opens new avenues of our understanding, particularly with the detection of gravitational waves and how these waves leave indelible marks on spacetime. This concept aligns well with what I’ve long believed: technology and science, when carefully wielded, have the power to reveal surprising and subtle wonders of our universe.

Gravitational Waves: More than Just Ripples

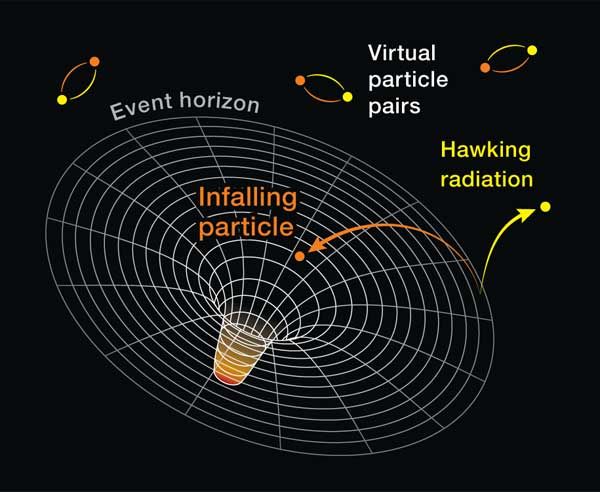
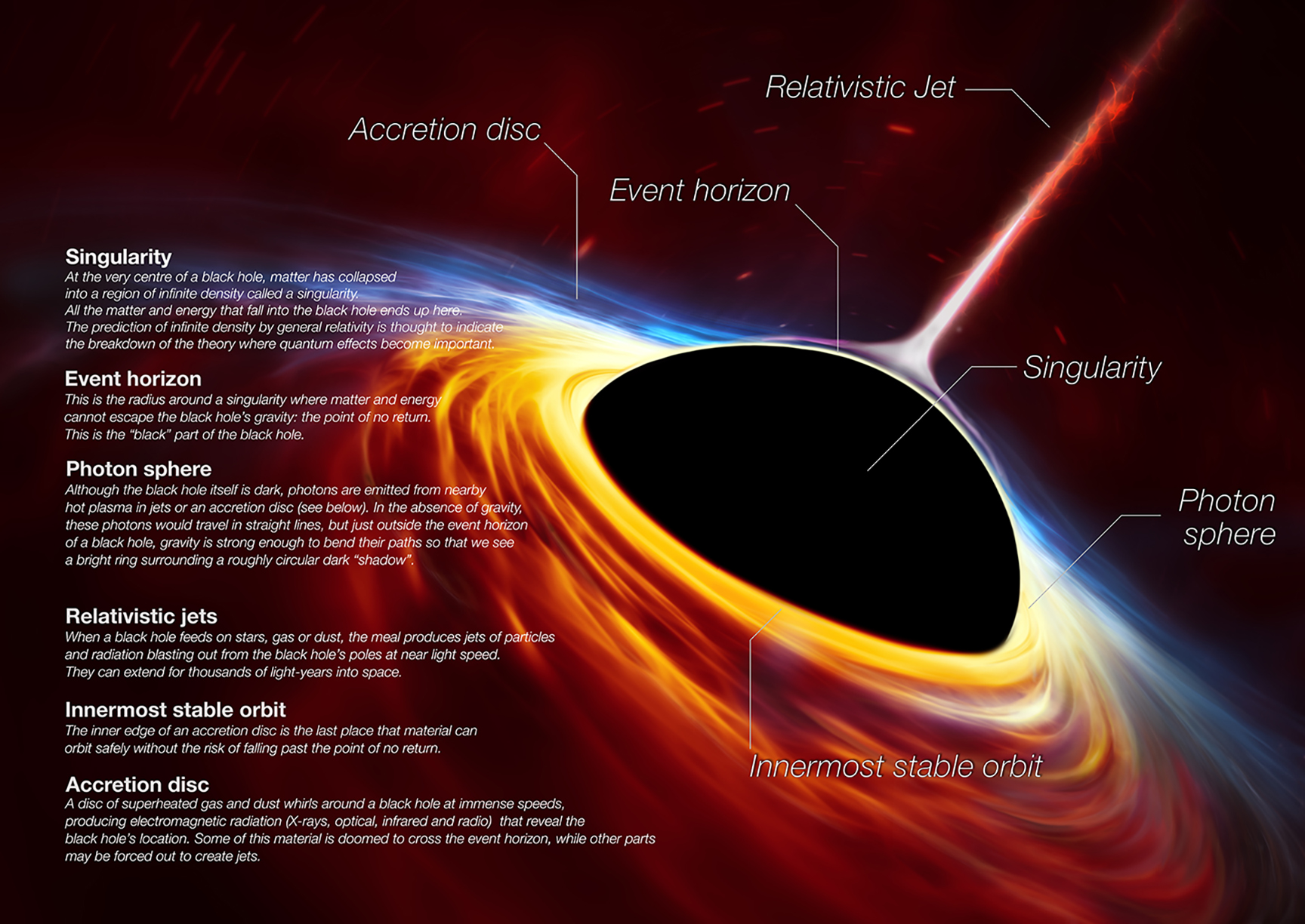
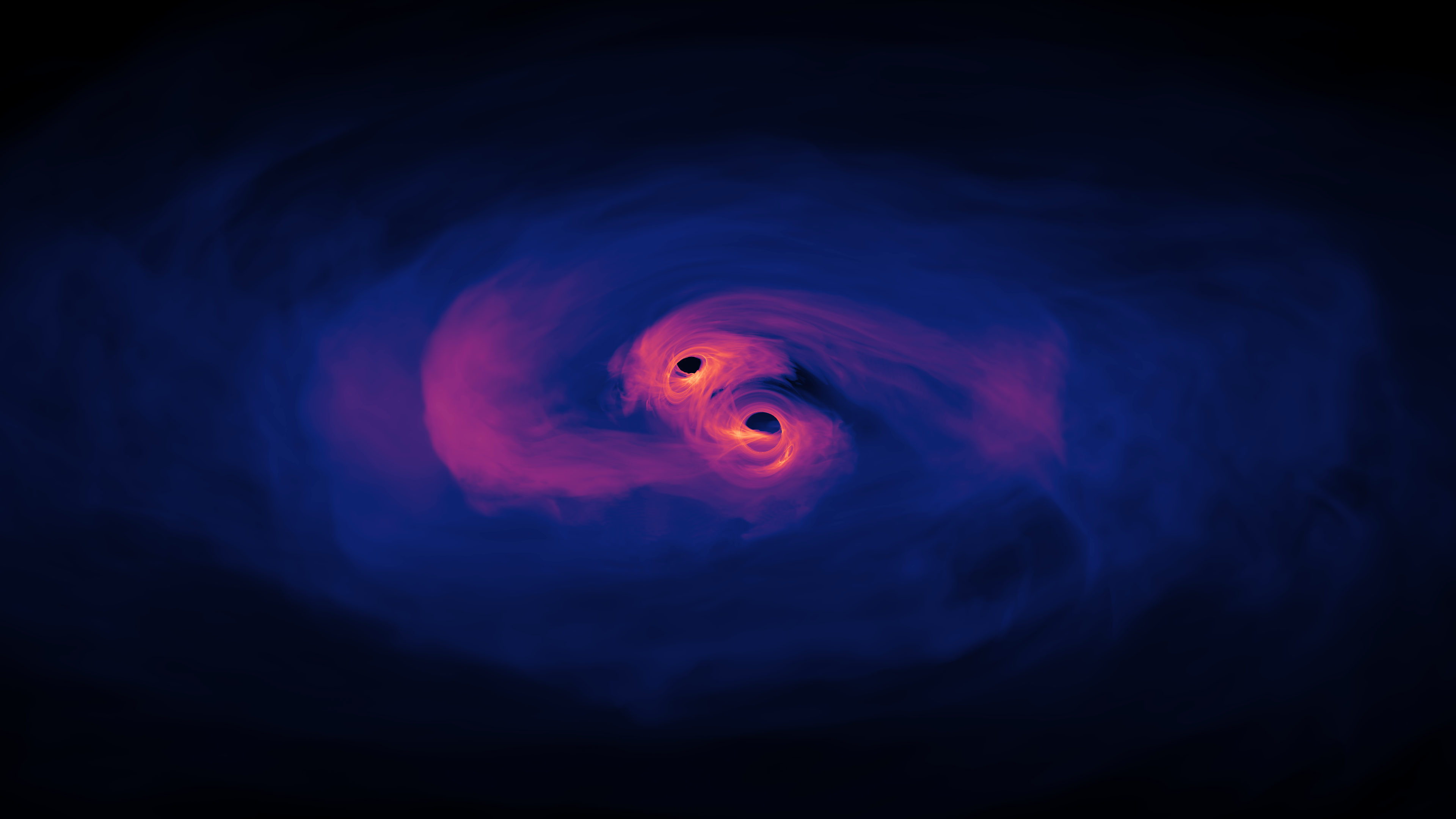
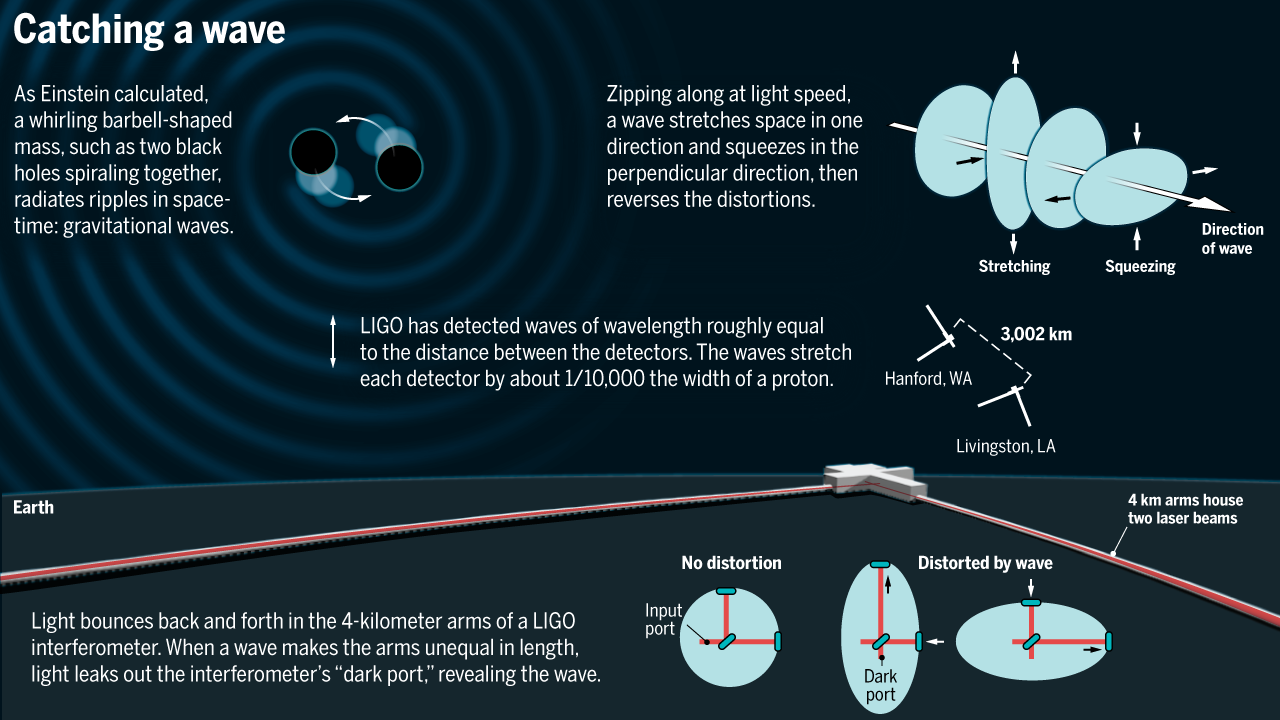
Gravitational waves are perturbations in the fabric of spacetime, predicted by Einstein’s theory of general relativity. When massive objects—such as black holes or neutron stars—accelerate, they send out ripples in spacetime. These waves distort distances along and perpendicular to their path as they pass through the universe. Today, with the groundbreaking work of observatories like LIGO and VIRGO, we’ve been able to detect these gravitational waves, especially those that are the result of black hole mergers or neutron star collisions.

However, the gravitational waves we’ve observed so far are simply “ripples.” They pass through spacetime without permanently altering it. Once the wave passes, spacetime “snaps back” to its original form—a concept we are familiar with in elastic physics. Similar to how a boat on a choppy lake bobs up and down with water ripples but returns to its starting position once calm sets in, gravitational waves do not leave lasting imprints.

But not all gravitational waves are created equal; there’s a deeper layer to this cosmic ballet. Enter the notion of gravitational memory, where instead of spacetime recovering its original form, it retains some “memory” or lasting impact of the event. This gravitational memory effect could teach us a great deal about recurring phenomena in the universe and even provide new insights into unexplained mysteries, like dark matter.

What Is Gravitational Memory and How Does It Work?

In simple terms, gravitational memory refers to the residual effects left on spacetime by a massive event, such as the merging of two black holes. Imagine a ring of stars affected by the passage of a gravitational wave. Initially, the stars oscillate together and apart, squishing and stretching under the gravitational influence. Normally, after the wave passes, the star positions would return to their original configuration. However, with gravitational memory, the stars may remain in a slightly altered configuration due to a residual wave effect, known as displacement memory.

There are different types of gravitational memory effects, such as:

Displacement Memory: This involves a permanent shift in the position of stars or other celestial bodies, as explained earlier.
Velocity-Kick Memory: Post-wave, objects may continue moving with an added “kick” velocity, comparable to how a tsunami drags water and boats along with it.
Gravitational Spin Memory: A more subtle effect occurs when an event imparts angular momentum to matter, twisting it in the direction of the wave.

Interestingly, gravitational memory is predicted with a very strong foundation in the mathematics of general relativity, and modern computational models support its existence. But despite our advancements in detecting regular gravitational waves, memory effects remain elusive because they are far weaker and harder to detect. Current detectors, like LIGO, are not yet sensitive enough to capture these non-elastic waveforms.

How Can We Detect Gravitational Memory?

Future technologies, such as the upcoming Laser Interferometer Space Antenna (LISA), will play a pivotal role in detecting gravitational memory. Led by the European Space Agency, LISA is scheduled to launch in 2035 and will comprise three satellites arranged in a triangular setup, each separated by an astonishing distance of 2.5 million kilometers. This vast array in space will allow it to detect low-frequency gravitational waves from events like supermassive black hole mergers—events much larger than what LIGO currently focuses on.

LISA will offer new precision in detecting the “displacement memory” effect. Simulations suggest that the difference in arm lengths in LISA’s detection setup may persist after the gravitational wave passes—a direct sign of gravitational memory. If one remembers our previous article on Sagittarius A* Image Analysis, we discussed at length how breakthroughs in AI and astronomy equip us with new perspectives. Much in the same way, LISA, combined with insights we can gather from memory effects, will serve as a new “lens” on cosmic events of the distant past.

Potential Discoveries through Gravitational Memory

Gravitational memory is more than just another validation of Einstein’s theories. Although our ability to measure gravitational memory could be seen as a continued homage to the man whose name is inextricably linked to modern physics, the real excitement comes from exploring how we might uncover new phenomena:

Refinement of General Relativity: Observing gravitational memory may reveal non-linear aspects of gravity that challenge current assumptions, offering new insights or even necessitating modifications to Einstein’s equations.
Alternative Theories to Dark Matter: Some theorists speculate that the elusive “memory” imprints might be related to unexplained gravitational discrepancies that we currently attribute to dark matter. If these non-linear effects align with unexplained gravitational phenomena, dark matter might need to be reconsidered.
Insight into the Early Universe: The detection of gravitational memory would also provide us with a way to study primordial gravitational waves from the early universe. This may even give us new clues about the Big Bang and cosmic inflation—the universe’s rapid expansion after its birth.

Clearly, the rewards of successfully detecting gravitational memory will be vast. Not only will we learn more about the nature of gravity itself, but we’ll also be able to trace these waves back to some of the most cataclysmic events the universe has ever witnessed.

Conclusion: A New Frontier in Understanding Cosmic Events

While gravitational waves may still be a somewhat abstract concept to many, it’s essential to realize that these waves contain crucial information about the universe’s history. As we discussed in previous topics like our Mysteries of Vanishing Astronomical Objects, our understanding of the universe relies on unveiling what is sometimes invisible to the human eye but detectable through precision instruments and creative scientific inquiry.

Gravitational memory effects represent a new frontier. A permanent mark left on spacetime ensures that the universe not only *remembers* its past but also provides future discoverers like us with evidence of that past. LISA and instruments like it will allow us to explore these cosmic memories, deciphering the archive of the universe etched into spacetime forever.

November 15, 2024/2 Comments/by David Maiolo

Artificial Intelligence (AI)

Exploring Wolfram’s Theory of Everything: Can the Universe Be a Giant Computer Program?

Exploring Wolfram’s Theory of Everything: Could the Universe Be a Giant Computer Program?

For several years, I’ve been asked to explore Stephen Wolfram’s “Theory of Everything”—a bold attempt to describe the fundamental workings of the universe through computational theory. Wolfram, a renowned computer scientist and creator of the popular Mathematica software, proposes that the universe operates like a computer program. What if, at its core, the universe follows a set of simple computational rules that give rise to the complex phenomena we observe today such as gravity, the Standard Model, and relativity? This notion connects closely to the simulation hypothesis, which speculates that our reality is a giant simulation. It’s an intriguing theory, but does it hold up under scientific scrutiny?

The Simulation Hypothesis and Computation in Physics

The basic idea behind Wolfram’s theory is simple, yet profound: the universe follows a set of fundamental rules, not unlike a computer algorithm. From these basic rules, everything—from the force of gravity to the behavior of subatomic particles—emerges. Wolfram’s approach is based on similar principles that underpin cellular automaton, where simple rules can generate surprisingly complex patterns.

But can we actually explain physics with computation? Wolfram suggests that you could conceptualize the universe in a manner similar to a cellular automaton—essentially a four-dimensional “code” that evolves step by step. This would mean that all aspects of the universe are, at some level, deterministic and computationally structured. Yet, despite the elegance of this idea, it faces significant hurdles when subjected to the rigorous demands of physics, particularly Einstein’s theory of relativity.

Challenges with General Relativity and Lorentz Symmetry

The main challenge with Wolfram’s theory is its compatibility with Einstein’s General Relativity. Relativity describes how space and time are intimately connected and varies based on an observer’s reference frame. One major problem with computational approaches is that they work in discrete steps—increments of space and time. However, according to relativity, these increments can’t remain hidden. If space and time were truly discrete, this would manifest observationally. Yet, there’s no evidence of such discreteness.

In an elegant illustration, think of a photon—a quantum of light. The energy of the photon depends on how it’s observed: its energy is higher if the observer is moving towards it, lower if moving away. In an inherently discrete computational model, issues arise because different observers would calculate unobserved gaps in the graph representing space. This disconnect prevents any computational model from approximating General Relativity in a way that respects all of Einstein’s symmetries.

This brings us to the concept of Lorentz Symmetry, a key pillar of General Relativity that ensures the same physical laws apply regardless of how fast you’re moving or where you are in space. Attempting to simulate this through computational methods like grids, graphs, or even Wolfram’s hypergraphs has, thus far, proven problematic.

Introducing Hypergraphs: A Way Forward?

Despite the difficulties, Wolfram has pressed forward and introduced the idea of hypergraphs as a potential solution. A hypergraph is a more complex version of a traditional graph, where sets of nodes (representing points in space-time) are connected in ways that circumvent the discretization problems of simpler models. According to Wolfram, hypergraphs may offer a way to reconcile computation with both space and matter without breaking the theory of relativity.

In 2020, Wolfram and his collaborators published a follow-up to address concerns about Lorentz symmetry. They’ve focused on how hypergraphs might solve the problem of preserving the symmetry requirements of relativity in a discrete structure. In principle, this should work similarly to another theory in physics known as “causal sets,” a respected attempt to describe space and time as a network of discrete points with causal relationships between them.

At this juncture, it’s worth noting that while Wolfram’s hypergraphs offer a clever solution, they still leave much unexplained. For instance, his framework for quantum mechanics, the behavior of elementary particles, and how exactly the Standard Model fits into the picture remains vague. This is an area I hope to see more developments on, as successful integration here would truly validate or break his theory’s foundation.

Looking Ahead: Are We Near a Theory of Everything?

Wolfram’s theory is an ongoing, evolving effort, and it’s not without merit. At the very least, it introduces novel approaches to theoretical physics and stimulates some intriguing discussions. However, it hasn’t reached a point where it effectively competes with established theories like General Relativity or String Theory. Incorporating quantum physics and providing stringent mathematical proofs for his model remains a significant challenge. Time will tell whether Wolfram’s work is able to capture the attention of mainstream physicists or if it will remain a curious side-note in the long and complicated quest for a “Theory of Everything.”

In conclusion, Wolfram’s theory is an ambitious attempt to bring the simulation hypothesis into the realm of physics. Does it answer all the questions? Certainly not yet. But given the originality and clarity of thought, it’s certainly worth paying more attention to. Perhaps, like many groundbreaking ideas, it will slowly gain traction as physicists grapple with its implications over time.

Relating to Previous Discussions on Fundamental Physics

Readers following my previous articles on quantum physics such as “Loop Quantum Gravity vs. String Theory” or on advances in “Understanding String Theory”, might notice a through line: physicists globally continue to grapple with how to marry quantum mechanics with relativity. Wolfram’s theory raises many of the same questions addressed in string theory, yet ventures into completely new territory by attempting to use computational rules to explain everything. Similar to how loop quantum gravity discretizes space-time, Wolfram’s hypergraph approach seeks to unify fundamental physics but with a key computational twist.

The importance of finding a Theory of Everything cannot be overstated. It’s the holy grail of physics. Whether Wolfram’s computational universe is that missing link remains an open question, but it certainly warrants more attention as physicists and mathematicians further explore it.

Focus Keyphrase: Wolfram’s Theory of Everything

October 25, 2024/2 Comments/by David Maiolo

Science News

Exploring the Universe with Loop Quantum Gravity: A New Perspective on Space-Time

Demystifying Loop Quantum Gravity: A Dive into the Quantum Fabric of the Universe

Amid the towering achievements and persistent mysteries of modern physics, one theory attempts to reconcile the monumental pillars of general relativity and quantum mechanics: Loop Quantum Gravity (LQG). As an avid enthusiast of physics, particularly quantum field theory, the exploration of the universe at its most fundamental level has always fascinated me. Loop Quantum Gravity, with its audacious aim to describe the quantum fabric of space-time itself, represents a thrilling frontier in theoretical physics. In this article, we will delve into the core concepts behind Loop Quantum Gravity, its implications, and why it stands out as a promising candidate for a theory of quantum gravity.

Understanding Space-Time as Quantized

At the heart of Loop Quantum Gravity is the concept that space-time is not a continuous fabric but consists of finite, discrete quanta. This concept fundamentally shifts our understanding from the smooth space-time described by Albert Einstein’s general relativity to a granular picture at the Planck scale (about \(10^{-35}\) meters).

LQG mathematically formulates this quantum space-time using what are termed “spin networks” – abstract graphs whose edges and nodes embody the quantum states of space-time geometry. These networks evolve over time, depicting a dynamic, quantized geometry that differs markedly from the static, continuous field of classical relativity.

The Role of Spin Networks and Spin Foams

Spin networks provide the skeleton of space in LQG, offering a snapshot of the quantum state of the gravitational field. Nodes within these networks represent quanta of space, while the edges depict the spatial relationships between them. Transitioning from one quantum state to another, spin networks evolve, thereby generating a history of geometrical changes. This history is chronicled by “spin foams”, which are the higher-dimensional analogs of spin networks, representing space-time’s quantum evolution.

Spin Network and Spin Foam representations

Through spin networks and spin foams, LQG introduces a quantum theory that is background-independent, meaning it does not presuppose the existence of a fixed space-time backdrop, aligning with the principle of general relativity that space-time’s geometry is dynamic.

Implications for Black Hole Physics and Early Universe Cosmology

Loop Quantum Gravity’s quantized vision of space-time has profound implications, particularly in the realms of black hole physics and the universe’s infancy. By applying LQG to these extreme conditions, researchers have derived tantalizing insights, such as the possibility that black holes have discrete, quantized areas. This quantization could potentially solve the black hole information paradox, suggesting information could be preserved rather than destroyed by black holes.

Quantized areas of a black hole in Loop Quantum Gravity

In early universe cosmology, LQG offers a glimpse into pre-Big Bang scenarios, proposing mechanisms that could explain the universe’s bounce from a previous, contracting phase to its current expansion, avoiding the classical singularity problem entailed by the Big Bang theory.

Challenges and the Path Forward

Despite its promising prospects, Loop Quantum Gravity faces significant challenges. Notably, deriving tangible predictions that can be tested experimentally has proven difficult, a hurdle that must be overcome to empirically validate the theory. Furthermore, reconciling LQG with the vast array of phenomena explained by quantum field theory and the Standard Model of particle physics remains an ongoing endeavor.

In conclusion, as we navigate this intricate dance of quantum mechanics and general relativity, Loop Quantum Gravity offers a compelling framework that challenges our conventional understanding of the universe. Its exploration embodies the essence of physics and philosophy – an unending quest to comprehend the cosmos’s fundamental nature. As someone deeply enamored by the mysteries of physics, following the advancements in Loop Quantum Gravity feels like participating in an epoch-defining journey, one that inches us closer to unlocking the universe’s ultimate secrets.

February 23, 2024/0 Comments/by David Maiolo

Science News

Exploring Hawking Radiation: A Key to Black Hole Mysteries

Delving into the Hawking Radiation: Unveiling Black Hole Mysteries

In an ever-expanding universe full of enigmatic celestial phenomena, black holes stand out as one of the most fascinating subjects for physicists and astronomers alike. My journey into astrophysics, albeit as a passionate enthusiast, has always drawn me towards these cosmic behemoths. They are not just a marvel to behold but also a treasure trove of physics extremes that challenge our understanding of the universe. Among the numerous phenomena associated with black holes, Hawking Radiation stands out for its quintessential role in demonstrating the intersection between quantum mechanics and gravitational theory.

Understanding Hawking Radiation

In 1974, Stephen Hawking proposed a groundbreaking theory that black holes are not entirely black but emit radiation due to quantum effects near the event horizon. This phenomenon, known as Hawking Radiation, introduces a fascinating paradox into the nature of black holes, proposing that they can lose mass and eventually evaporate over time. The concept starts with the idea that the vacuum in quantum field theory is filled with temporary pairs of particles and antiparticles that form and annihilate in incredibly short timescales.

Near the event horizon of a black hole, however, something remarkable occurs. If a pair of such particles forms, one can fall into the black hole while the other escapes. The escaped particle adds energy to the universe, while the one captured subtracts mass from the black hole, as per Einstein’s equation \(E = mc^2\). Hence, the black hole loses mass through this process of particle escape, a compelling yet eerie evanescence we now refer to as Hawking Radiation.

The Equation Behind Hawking Radiation

The phenomenon is described mathematically by the equation:
\[ HR = \frac{\hbar c^6}{15360 \pi G^2 M^2} \]
where \(HR\) is the Hawking Radiation power, \(\hbar\) is the reduced Planck’s constant, \(c\) is the speed of light, \(G\) is the gravitational constant, and \(M\) is the mass of the black hole. This equation suggests that the radiation power is inversely proportional to the square of the mass of the black hole, indicating that smaller black holes radiate more powerfully.

Implications on Physics and Black Hole Paradoxes

One of the most tantalizing aspects of Hawking Radiation lies in its ability to bridge the gap between quantum mechanics and general relativity. It suggests a mechanism through which black holes not only emit radiation but also ultimately evaporate, posing fascinating questions about what happens to the information trapped inside a black hole. This is central to the black hole information paradox, a hotly debated topic in theoretical physics. Do the remnants of Hawking Radiation contain any information about the matter that fell into the black hole, or is it lost forever? The debate continues, fueling research and discussions in the scientific community.

Personal Reflections

My interest in astrophysics, though purely from the stance of an enthusiast, finds a peculiar charm in the contemplation of black holes and their mysteries. The sheer scale of ideas, from quantum fluctuations to the fabric of spacetime, captivates my imagination. Moreover, as someone deeply rooted in the realm of technology and artificial intelligence, I ponder over the parallels between decoding the mysteries of the cosmos and unlocking the potential of AI. Both realms challenge us to extend beyond our current understandings, pushing the boundaries of possible knowledge.

Traveling to places like Hawaii with my telescope, capturing the night sky, has been a cherished activity among my group of amateur astronomer friends. It’s during these stargazing sessions, under the serene, star-filled skies, that I reflect on the incredible work of physicists like Stephen Hawking and the profound mysteries they’ve unveiled. It’s a humbling reminder of the vastness of our universe and the pursuit of knowledge that drives us.

Conclusion

Hawking Radiation exemplifies the profound beauty of physics — its ability to unify seemingly unrelated domains (quantum mechanics and gravity) through a principle that challenges our understanding of the universe. As we continue to decode the mysteries encapsulated within black holes, we edge closer to answering some of the most fundamental questions about our universe’s very fabric. In this endeavor, Hawking Radiation stands as a beacon of our quest for knowledge, a testament to human curiosity and the unyielding quest to understand our cosmos.

For further exploration into the cosmos and the intriguing interplay between different scientific realms, consider visiting some of my recent posts on https://www.davidmaiolo.com, where I delve into various aspects of technology, AI, and their applications in understanding our universe.

References & Further Reading

Hawking, S. W. (1974). Black hole explosions? Nature, 248(5443), 30-31.
Misner, C. W., Thorne, K. S., & Wheeler, J. A. (1973). Gravitation. New York: W. H. Freeman and Company.
Wald, R. M. (1984). General Relativity. University of Chicago Press.

February 17, 2024/0 Comments/by David Maiolo