Tag Archive for: optimization algorithms

Understanding the Impact of Gradient Descent in AI and ML

The Integral Role of Calculus in Artificial Intelligence and Machine Learning

In the vast and constantly evolving fields of Artificial Intelligence (AI) and Machine Learning (ML), the significance of foundational mathematical concepts cannot be overstated. Among these, Calculus, specifically, plays a pivotal role in shaping the algorithms that are at the heart of AI and ML models. In this article, we’ll delve into a specific concept within Calculus that is indispensable in AI and ML: Gradient Descent. Moreover, we will illustrate how this mathematical concept is utilized to solve broader problems, a task that aligns perfectly with my expertise at DBGM Consulting, Inc.

Understanding Gradient Descent

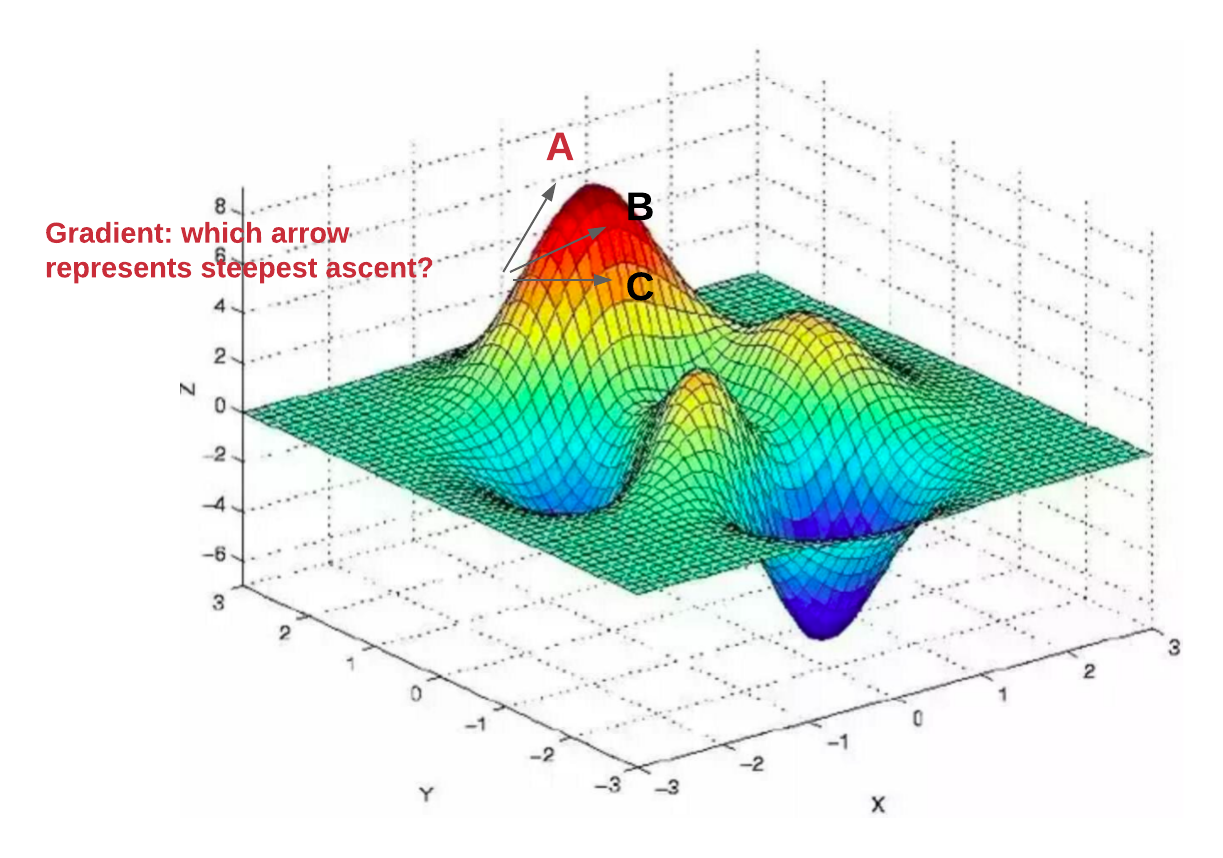
Gradient Descent is a first-order iterative optimization algorithm used to minimize a function. In essence, it involves taking small steps in the direction of the function’s steepest descent, guided by its gradient. The formula used to update the parameters in Gradient Descent is given by:

θ = θ - α ∇θ J(θ)

where:

  • θ represents the parameters of the function or model.
  • α is the learning rate, determining the size of the steps taken.
  • ∇θ J(θ) is the gradient of the objective function J(θ) with respect to the parameters θ.

This optimization method is particularly vital in the field of ML, where it is used to minimize the loss function, adjusting the weights of the network to improve prediction accuracy.

Application in AI and ML

Considering my background in developing machine learning models for self-driving robots at Harvard University, the application of Gradient Descent is a daily reality. For instance, in ensuring that an autonomous vehicle can correctly interpret its surroundings and make informed decisions, we optimize algorithms to discern patterns within vast datasets, an endeavor where Gradient Descent proves invaluable.

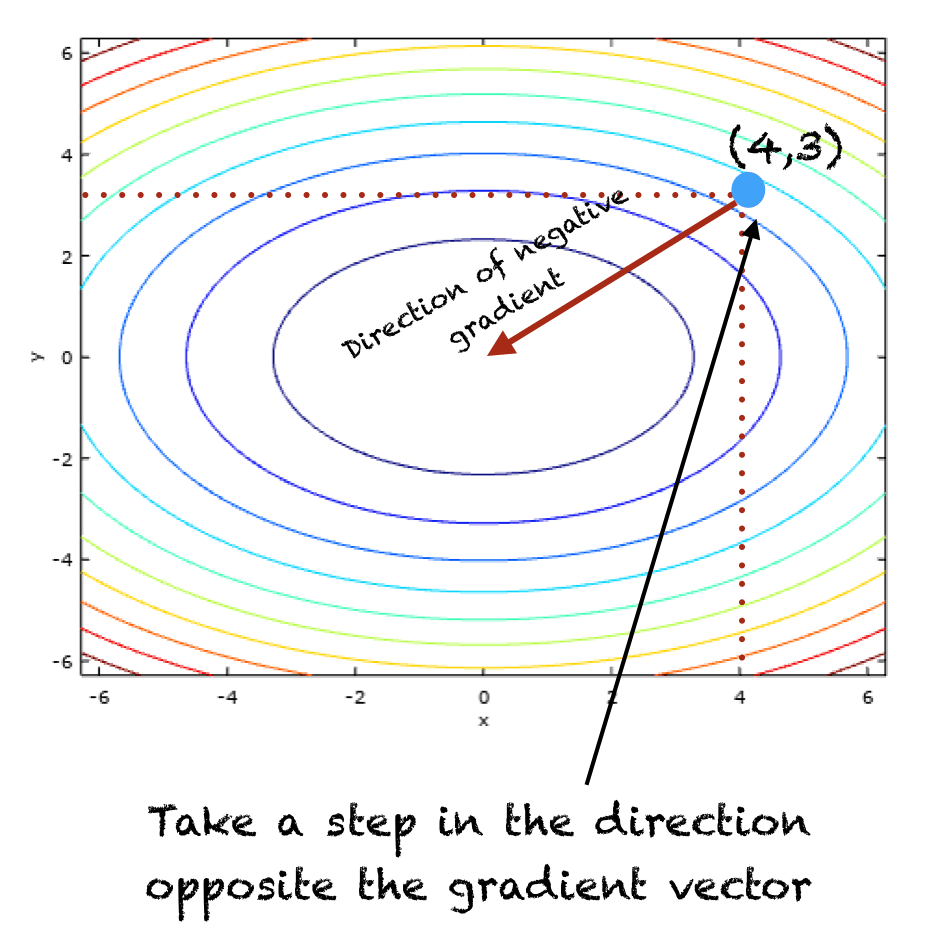
Gradient Descent example in machine learning

The iterative nature of Gradient Descent, moving steadily towards the minimum of a function, mirrors the process of refining an AI model’s accuracy over time, by learning from data and adjusting its parameters accordingly. This optimization process is not just limited to robotics but extends across various domains within AI and ML such as natural language processing, computer vision, and predictive analytics.

Connecting Calculus to Previous Discussions

In light of our prior exploration into concepts like Large Language Models (LLMs) and Bayesian Networks, the underpinning role of Calculus, especially through optimization techniques like Gradient Descent, reveals its widespread impact. For example, optimizing the performance of LLMs, as discussed in “Exploring the Future of Large Language Models in AI and ML,” necessitates an intricate understanding of Calculus to navigate the complexities of high-dimensional data spaces effectively.

Moreover, our delve into the mathematical foundations of machine learning highlights how Calculus not only facilitates the execution of complex algorithms but also aids in conceptualizing the theoretical frameworks that empower AI and ML advancements.

Conclusion

Gradient Descent exemplifies the symbiotic relationship between Calculus and the computational models that drive progress in AI and ML. As we continue to push the boundaries of what AI can achieve, grounding our innovations in solid mathematical understanding remains paramount. This endeavor resonates with my vision at DBGM Consulting, where leveraging deep technical expertise to solve real-world problems forms the cornerstone of our mission.

Focus Keyphrase: Gradient Descent in AI and ML

/2 Comments/by

Exploring Gradient Descent: The Heart of AI and ML Optimization

Unlocking the Secrets of Optimization: Exploring Gradient Descent

In the realm of mathematics and computer science, the concept of optimization stands as a cornerstone for numerous advancements and innovations. Today, I dive into one of the most pivotal optimization algorithms that has significantly molded the landscape of Artificial Intelligence (AI) and Machine Learning (ML)—Gradient Descent. Having applied this very concept in developing machine learning models during my time at Harvard University, I’ve firsthand witnessed its transformative power.

Understanding Gradient Descent

Gradient Descent is an iterative optimization algorithm used to minimize a function by iteratively moving in the direction of the steepest descent as defined by the negative of the gradient. In simpler terms, it’s used to find the minimum value of a function. The beauty of Gradient Descent lies in its simplicity and efficiency, making it the algorithm of choice for many machine learning problems.

The mathematical expression for updating the parameters in Gradient Descent is:

θ = θ - α * ∇F(θ)

where:

  • θ represents the parameters of the function we’re trying to minimize,
  • α denotes the learning rate, determining the size of the steps taken towards the minimum,
  • ∇F(θ) is the gradient of the function at θ.

Application in AI and ML

In the context of AI and my specialization in Machine Learning models, Gradient Descent plays a pivotal role in training models. By minimizing the loss function, which measures the difference between the model’s predicted output and the actual output, Gradient Descent helps in adjusting the model’s parameters so that the model can make more accurate predictions.

Case Study: Machine Learning for Self-Driving Robots

During my postgraduate studies, I engaged in a project developing machine learning algorithms for self-driving robots. The challenge was to create an algorithm that could accurately predict the robot’s movements in an unknown environment. Employing Gradient Descent, we minimized the loss function of our model, which was pivotal in accurately predicting the robot’s next move based on sensor inputs.

Why Gradient Descent?

Gradient Descent is favored in machine learning due to its capability to handle large datasets efficiently. As data becomes the lifeblood of AI, the ability to process and learn from vast datasets is crucial. Gradient Descent, with its scalable nature, stands out by offering a means to effectively optimize complex models without the need for computationally expensive operations.

Visualization of Gradient Descent

Understanding Gradient Descent isn’t only about the numbers and algorithms; visualizing its process can significantly enhance comprehension. Here’s how a typical Gradient Descent optimization might look when visualized:

Gradient Descent visualization

Conclusion

Gradient Descent is more than just a mathematical equation; it’s a bridge between theoretical mathematics and practical application in the field of Artificial Intelligence. As we push the boundaries of what machines can learn and do, understanding and applying concepts like Gradient Descent becomes increasingly important. In the intersection of complex algorithms and real-world applications, it continues to be a beacon of innovation, driving the development of AI and ML forward.

In the spirit of continuous exploration, I invite readers to delve deeper into how optimization techniques are revolutionizing other fields. Consider visiting my previous posts on Numerical Analysis and its significant impact on AI and machine learning for further reading.

/0 Comments/by

Unraveling Polynomial Equations with Newton’s Method in AI and ML

Deciphering the Roots: A Numerical Analysis Perspective on Polynomial Equations

In the realm of numerical analysis, one of the most captivating quests involves finding the roots of polynomial equations. These equations, which represent myriad phenomena across disciplines, are the foundation upon which both classical and contemporary science and engineering are built. The importance of polynomial roots in computational fields, especially in Artificial Intelligence (AI) and Machine Learning (ML), cannot be overstated—they serve as key components in algorithms essential for optimization, modeling, and solving complex systems. Today, I will delve into one specific method within numerical analysis that has transformed our approach to these problems: Newton’s Method.

Understanding Newton’s Method

At its core, Newton’s Method (also known as the Newton-Raphson method) offers a powerful approach to finding successively better approximations to the roots (or zeroes) of a real-valued function. Here’s the formula that underpins this method:

Xn+1 = Xn – f(Xn)/f'(Xn)

This iterative formula suggests that if you start with an initial guess X0 that is close to the true root, you can apply this formula repeatedly to get closer and closer to the actual root of the equation. This method is particularly appealing for its simplicity and the rapid convergence it offers under favorable conditions.

Application in AI and Machine Learning

In my practice at DBGM Consulting, Inc., leveraging the power of AI and ML to solve real-world problems is paramount. Newton’s Method comes into play especially in optimization problems where we need to find the minimum or maximum of a function—which, in essence, can be transformed into a root-finding problem. For instance, in the training phase of machine learning models, optimization algorithms like gradient descent are used to minimize a cost function. Newton’s Method enhances these algorithms by providing a more efficient way to converge towards the function’s minima, thereby improving the model’s performance.

Breaking Down the Mathematics

Let’s consider a polynomial equation f(x) = x3 – 7x2 + 8x – 3 and an initial guess X0=1.5. The goal is to find a root of f(x) using Newton’s Method. The derivative of f(x), needed for our formula, is f'(x) = 3x2 – 14x + 8. Applying the Newton’s formula iteratively, we find improved approximations of the root with each step, eventually converging to a solution that, while approximate, is incredibly close to the actual root.

Challenges and Considerations

While Newton’s Method is powerful, it’s not without its challenges. The method requires a derivative, which might be difficult or impractical to obtain for complex functions. Moreover, the initial guess X0 has to be reasonably close to the true root for the method to converge. Additionally, the method does not guarantee convergence for all functions, highlighting the need for careful analysis and potentially alternative approaches in such cases.

Concluding Thoughts

The elegance of Newton’s Method in numerical analysis lies in its ability to simplify the seemingly daunting task of root-finding to iterative formula application. In AI and ML, where optimization is frequently at the heart of problem-solving, understanding and applying this method can significantly enhance algorithm efficiency and effectiveness. As we continue to push the boundaries of what these technologies can achieve, the foundations laid by numerical analysis methods like this one play an instrumental role in driving progress.

As I reflect on my journey from a Harvard University graduate focusing on information systems and AI, through my experiences at Microsoft, and into the establishment of my own firm, the unifying thread has been the constant pursuit of applying such mathematical principles to solve real-world challenges. Whether optimizing machine learning models or developing innovative cloud solutions, the essence of numerical analysis remains a cornerstone of technological advancement.

<Newton's Method Graphical Illustration>
<Optimization curves in Machine Learning>
<Real-life example of root-finding application in AI>

I invite you to explore further instances where mathematical elegance meets practical application across various fields on my blog. Let’s continue to unravel the complexity of our world, one equation at a time.

/0 Comments/by
Link to: Get in touch

Let’s collaborate!

Contact Me

DAVID MAIOLO

 The content on this website, including text, photographs, and any other media, is the property of David Maiolo unless otherwise noted. No part of this website may be reproduced, distributed, or transmitted in any form or by any means, including photocopying, recording, or other electronic or mechanical methods, without the prior written permission of the owner.

DISCLAIMER

The information provided on this website is for general informational purposes only. While I strive to keep the information up-to-date and correct, I make no representations or warranties of any kind, express or implied, about the completeness, accuracy, reliability, suitability, or availability with respect to the website or the information, products, services, or related graphics contained on the website for any purpose. Any reliance you place on such information is therefore strictly at your own risk. In no event will I be liable for any loss or damage including without limitation, indirect or consequential loss or damage, or any loss or damage whatsoever arising from loss of data or profits arising out of, or in connection with, the use of this website. *This website may include links to other websites which are not under the control of David Maiolo. I have no control over the nature, content, and availability of those sites.

© 2024 David Maiolo