The Role of Fine-Tuning Metrics in the Evolution of AI
Artificial Intelligence (AI) has flourished by refining its models based on various metrics that help determine the optimal outcome for tasks, whether that’s generating human-like language with chatbots, forecasting business trends, or navigating self-driving robots accurately. Fine-tuning these AI models to achieve accurate, efficient systems is where the real power of AI comes into play. As someone with a background in AI, cloud technologies, and machine learning, I’ve seen first-hand how essential this process is in advanced systems development. But how do we define “fine-tuning,” and why does it matter?
What is Fine-Tuning in AI?
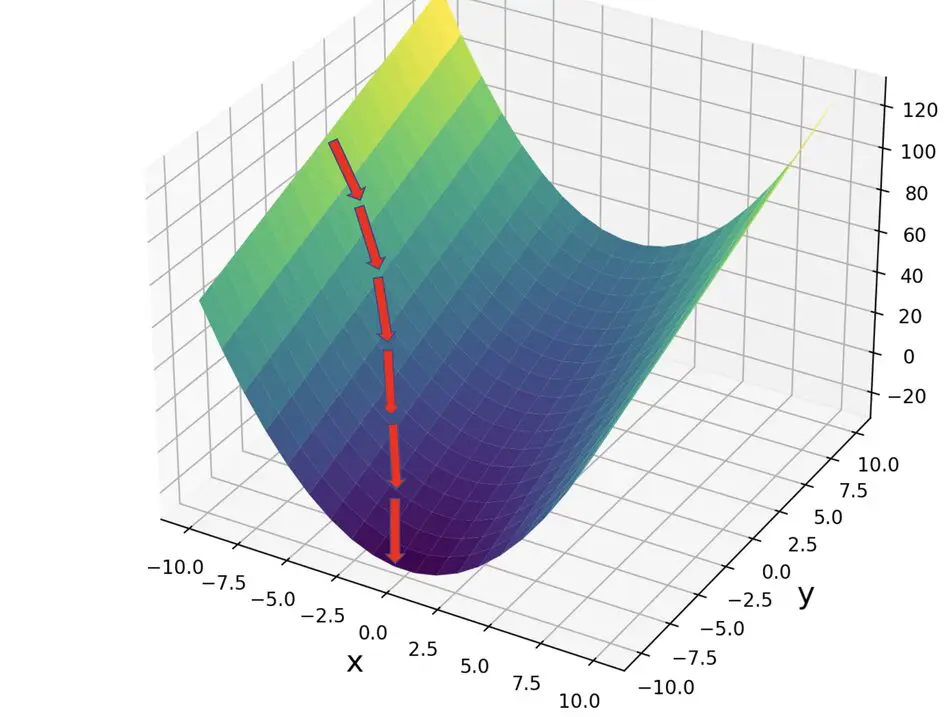
In essence, fine-tuning refers to adjusting the parameters of an AI model to improve performance after its initial training. Models, such as those found in supervised learning, are first trained on large datasets to grasp patterns and behaviors. But often, this initial training only gets us so far. Fine-tuning allows us to optimize the model further, improving accuracy in nuanced situations and specific environments.
A perfect example of this process is seen in neural machines used for self-driving cars, a space I’ve been directly involved with throughout my work in machine learning. Imagine the complexity of teaching a neural net to respond differently in snowy conditions versus clear weather. Fine-tuning ensures that the car’s AI can make split-second decisions, which could literally be the difference between a safe journey and an accident.
Real-world Applications of AI Fine-Tuning
Fine-tuning isn’t just about making AI models more accurate – its usefulness stretches far and wide across industries. Here are a few major applications based on my consulting experience:
- Autonomous Driving: Self-driving vehicles rely heavily on fine-tuned algorithms to detect lanes, avoid obstacles, and interpret traffic signals. These models continuously improve as they gather more data.
- AI-Powered Customer Service: AI-driven chatbots need continuous optimization to interpret nuanced customer inquiries, ensuring they’re able to offer accurate information that is context-appropriate.
- Healthcare Diagnosis: In healthcare AI, diagnostic systems rely on fine-tuned models to interpret medical scans and provide differential diagnoses. This is especially relevant as these systems benefit from real-time data feedback from actual hospitals and clinics.
- Financial Models: Financial institutions use machine learning to predict trends or identify potential fraud. The consistency and accuracy of such predictions improve over time through fine-tuning of the model’s metrics to fit specific market conditions.
In each of these fields, fine-tuning drives the performance that ensures the technology doesn’t merely work—it excels. As we incorporate this concept into our AI-driven future, the importance of fine-tuning becomes clear.
The Metrics That Matter
The key to understanding AI fine-tuning lies in the specific metrics we use to gauge success. As an example, let’s look at the metrics that are commonly applied:
| Metric | Application |
|---|---|
| Accuracy | The number of correct predictions divided by the total number of predictions. Crucial in fields like healthcare diagnosis and autonomous driving. |
| Precision/Recall | Precision is how often your AI is correct when it makes a positive prediction. Recall measures how well your AI identifies positive cases—important in systems like fraud detection. |
| F1 Score | A balance between precision and recall, the F1 score is often used when the cost of false positives and false negatives bares more significance. |
| Logarithmic Loss (Log Loss) | This measures how uncertain our model is, with systems aiming to minimize log loss in real-world applications like risk assessment. |
It’s important to understand that each type of task or industry will have its own emphasis on what metrics are most relevant. My own work, such as conducting AI workshops for companies across various industries, emphasizes finding that sweet spot of fine-tuning based on the metrics most critical to driving business or societal goals.
Challenges in Fine-Tuning AI Models
Although fine-tuning can significantly improve AI performance, it isn’t without its challenges. Here are a few hurdles that professionals, including myself, often encounter when working with deep learning models:
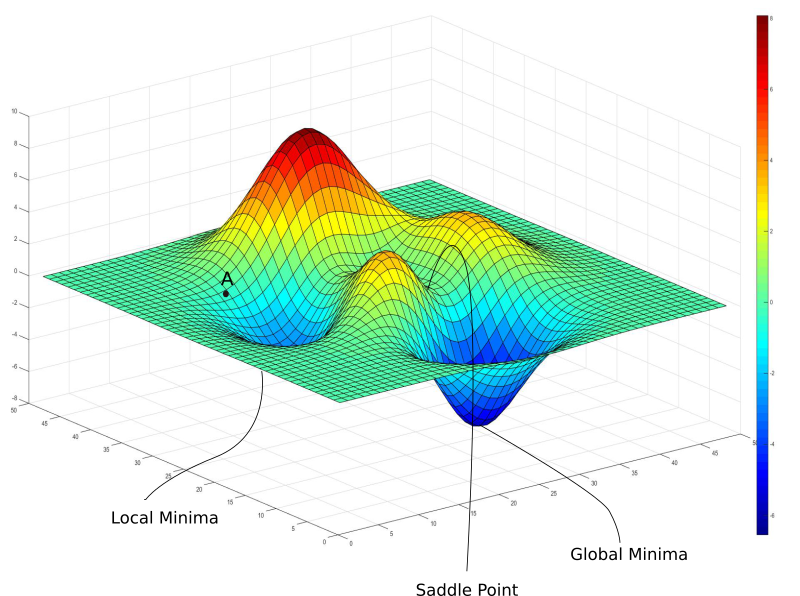
- Overfitting: The more you optimize a model to a certain dataset, the higher the risk that it becomes overfitted to that data, reducing its effectiveness on new, unseen examples.
- Data and Model Limitations: While large datasets help with better training, high-quality data is not always available, and sometimes what’s relevant in one region or culture may not be applicable elsewhere.
- Computational Resources: Some fine-tuning requires significant computational power and time, which can strain resources, particularly in smaller enterprises or startups.
Precautions When Applying AI Fine-Tuning
Over the years, I’ve realized that mastering fine-tuning is about not pushing too hard or making assumptions about a model’s performance. It is critical to understand these key takeaways when approaching the fine-tuning process:
- Focus on real-world goals: As I’ve emphasized during my AI and process automation consultations through DBGM Consulting, understanding the exact goal of the system—whether it’s reducing error rates or improving speed—is crucial when fine-tuning metrics.
- Regular Monitoring: AI systems should be monitored constantly to ensure they are behaving as expected. Fine-tuning is not a one-off process but rather an ongoing commitment to improving on the current state.
- Collaboration with Domain Experts: Working closely with specialists from the domain (such as physicians in healthcare or engineers in automobile manufacturing) is vital for creating truly sensitive, high-impact AI systems.
The Future of AI Fine-Tuning
Fine-tuning AI models will only become more critical as the technology grows and applications become even more deeply integrated with real-world problem solving. In particular, industries like healthcare, finance, automotive design, and cloud solutions will continue to push boundaries. Emerging AI technologies such as transformer models and multi-cloud integrations will rely heavily on an adaptable system of fine-tuning to meet evolutionary demands efficiently.

As AI’s capabilities and limitations intertwine with ethical concerns, we must also fine-tune our approaches to evaluating these systems. Far too often, people talk about AI as though it represents a “black box,” but in truth, these iterative processes reflect both the beauty and responsibility of working with such advanced technology. For instance, my ongoing skepticism with superintelligence reveals a cautious optimism—understanding we can shape AI’s future effectively through mindful fine-tuning.
For those invested in AI’s future, fine-tuning represents both a technical challenge and a philosophical question: How far can we go, and should we push the limits?
Looking Back: A Unified Theory in AI Fine-Tuning
In my recent blog post, How String Theory May Hold the Key to Quantum Gravity and a Unified Universe, I discussed the possibilities of unifying the various forces of the universe through a grand theory. In some ways, fine-tuning AI models reflects a similar quest for unification. Both seek a delicate balance of maximizing control and accuracy without overloading their complexity. The beauty in both lies not just in achieving the highest level of precision but also in understanding the dynamic adjustments required to evolve.

If we continue asking the right questions, fine-tuning might just hold the key to our most exciting breakthroughs, from autonomous driving to solving quantum problems.


 >
> >
> >
>