Exploring the Mathematical Foundations of Neural Networks Through Calculus

In the world of Artificial Intelligence (AI) and Machine Learning (ML), the essence of learning rests upon mathematical principles, particularly those found within calculus. As we delve into the intricacies of neural networks, a foundational component of many AI systems, we uncover the pivotal role of calculus in enabling these networks to learn and make decisions akin to human cognition. This relationship between calculus and neural network functionality is not only fascinating but also integral to advancing AI technologies.

The Role of Calculus in Neural Networks

At the heart of neural networks lies the concept of optimization, where the objective is to minimize or maximize an objective function, often referred to as the loss or cost function. This is where calculus, and more specifically the concept of gradient descent, plays a crucial role.

Gradient descent is a first-order optimization algorithm used to find the minimum value of a function. In the context of neural networks, it’s used to minimize the error by iteratively moving towards the minimum of the loss function. This process is fundamental in training neural networks, adjusting the weights and biases of the network to improve accuracy.

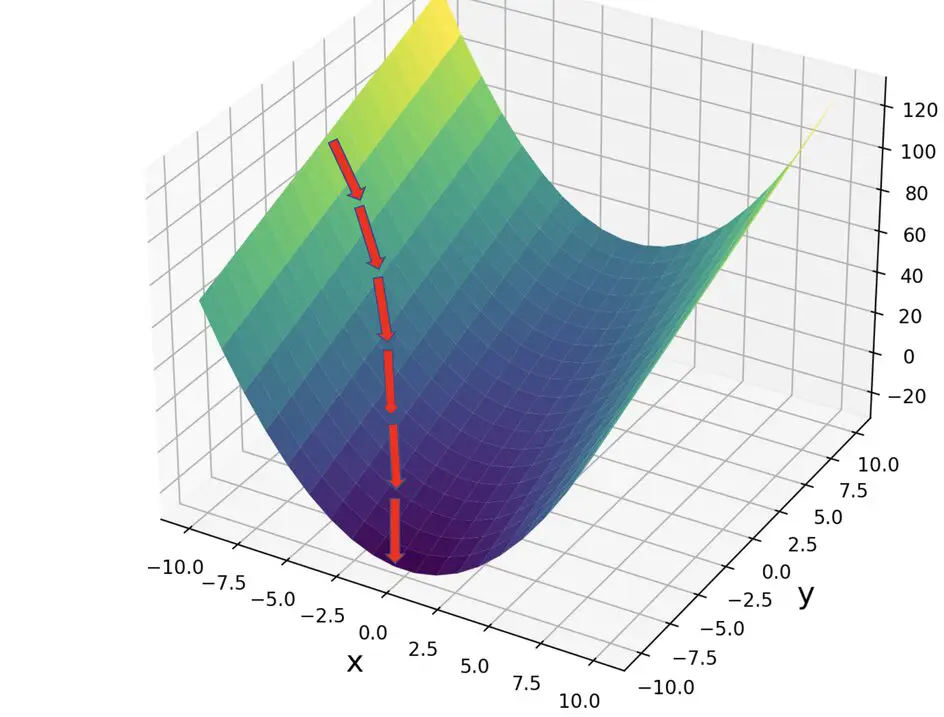
Understanding Gradient Descent Mathematically

The method of gradient descent can be mathematically explained using calculus. Given a function f(x), its gradient ∇f(x) at a point x is a vector pointing in the direction of the steepest increase of f. To find the local minimum, one takes steps proportional to the negative of the gradient:

x_new = x_old – λ∇f(x_old)

Here, λ represents the learning rate, determining the size of the steps taken towards the minimum. Calculus comes into play through the calculation of these gradients, requiring the derivatives of the cost function with respect to the model’s parameters.

Practical Application in AI and ML

As someone with extensive experience in developing AI solutions, the practical application of calculus through gradient descent and other optimization methods is observable in the refinement of machine learning models, including those designed for process automation and the development of chatbots. By integrating calculus-based optimization algorithms, AI models can learn more effectively, leading to improvements in both performance and efficiency.

Linking Calculus to AI Innovation

Previous articles such as “Understanding the Impact of Gradient Descent in AI and ML” have highlighted the crucial role of calculus in the evolution of AI and ML models. The deep dive into gradient descent provided insights into how fundamental calculus concepts facilitate the training process of sophisticated models, echoing the sentiments shared in this article.

Conclusion

The exploration of calculus within the realm of neural networks illuminates the profound impact mathematical concepts have on the field of AI and ML. It exemplifies how abstract mathematical theories are applied to solve real-world problems, driving the advancement of technology and innovation.

As we continue to unearth the capabilities of AI, the importance of foundational knowledge in mathematics, particularly calculus, remains undeniable. It serves as a bridge between theoretical concepts and practical applications, enabling the development of AI systems that are both powerful and efficient.

Focus Keyphrase: calculus in neural networks