Applying Fermat’s Little Theorem in Cryptography: A Number Theory Perspective

In the realm of Number Theory, an area of mathematics that has fascinated scholars for centuries, certain theorems stand out for their utility and elegance. Fermat’s Little Theorem is one such result, offering insights into the properties of prime numbers that are crucial for modern computational algorithms, including those in the field of cybersecurity and cryptography. As an individual whose expertise spans across artificial intelligence, cloud solutions, and security, I find the application of mathematical theories like Fermat’s Little Theorem particularly compelling in the way they intersect with technological advancements to enhance data security.

Understanding Fermat’s Little Theorem

Fermat’s Little Theorem states that if p is a prime number, then for any integer a such that a is not divisible by p, it is the case that a^p ≡ a (mod p). In simpler terms, when a is raised to the power of p and then divided by p, the remainder is a. This theorem plays a foundational role in understanding the behavior of numbers in modular arithmetic, an essential part of the cryptographic algorithms that protect our digital communications.

<>

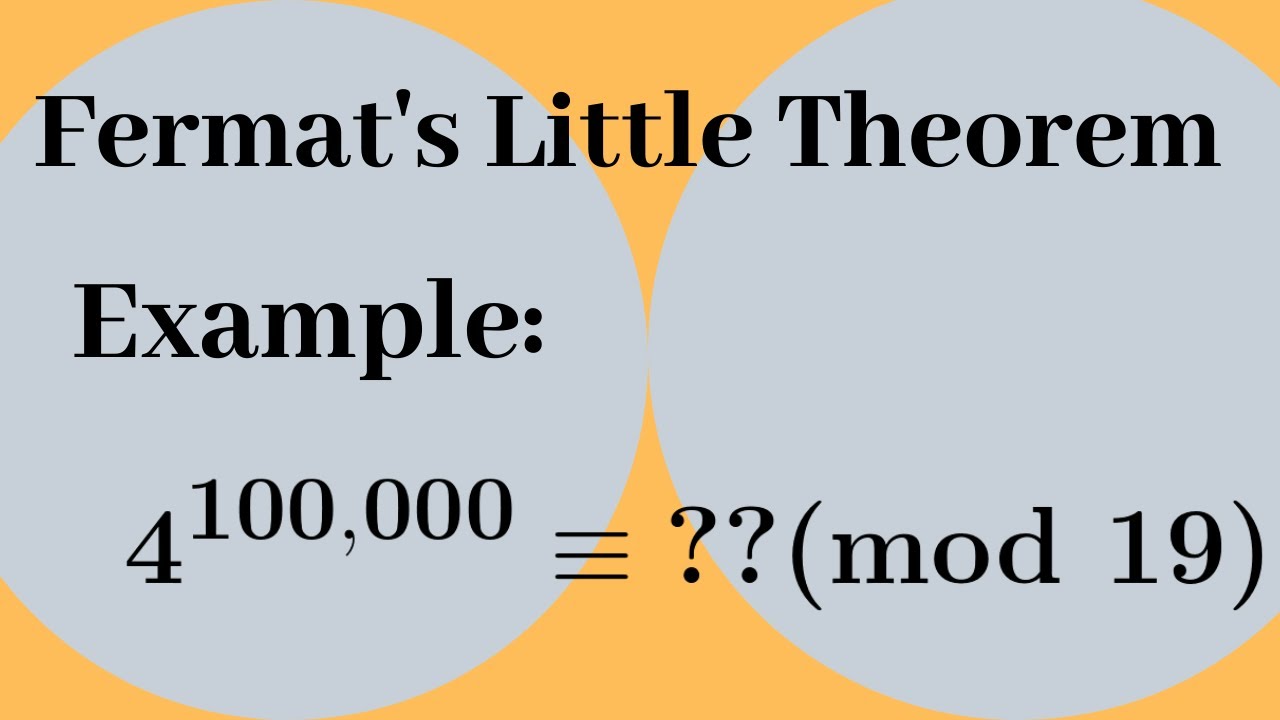Formula Representation

To visually represent the theorem, the mathematical formula can be stated as:

ap ≡ a (mod p)

Where:

• p is a prime number.
• a is an integer not divisible by p.

Application in Cryptography

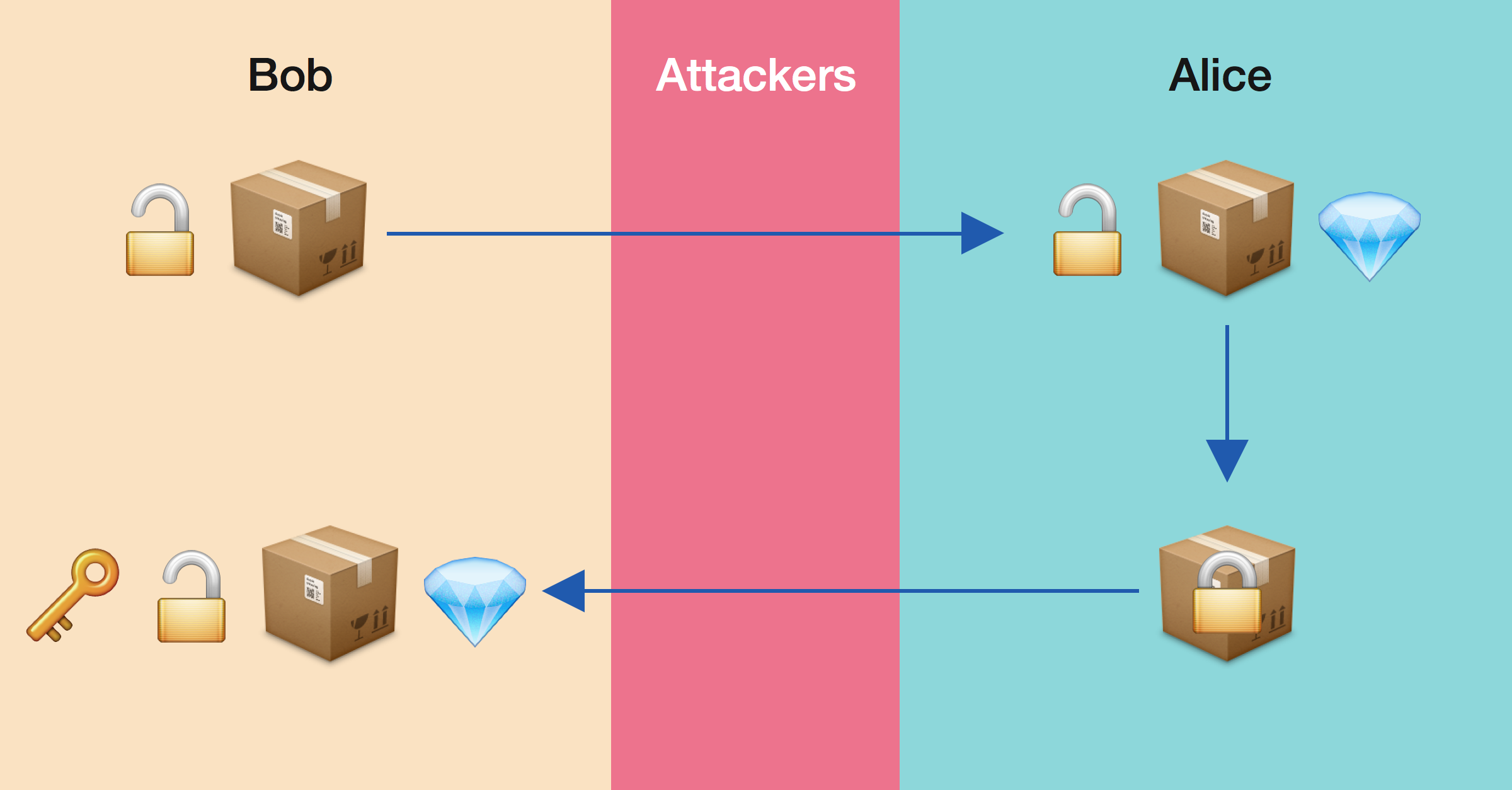
The true power of Fermat’s Little Theorem unfolds in its application within the field of cryptography, particularly in the generation and encryption of digital signatures and public-key encryption schemes like RSA (Rivest-Shamir-Adleman algorithm). The RSA algorithm, for instance, relies on the properties of large prime numbers and modular exponentiation, directly incorporating concepts from Fermat’s theorem.

When creating a public RSA key, two large prime numbers are chosen and multiplied together. Fermat’s Little Theorem assists in ensuring that these numbers have properties that make the encryption secure yet feasible to compute for those with the correct key. The theorem aids in determining the modular inverse during the RSA key generation process, crucial for decrypting the received messages.

<>

Linking Number Theory to Modern Challenges

The beauty of number theory, as demonstrated through Fermat’s Little Theorem, is its timeless relevance. As discussed in my previous articles, such as “Delving Deeper into the Mathematical Foundations of Machine Learning” and “Unlocking Complex AI Challenges with Structured Prediction and Large Language Models”, the intersection of mathematical theories with technological advancements offers a fertile ground for innovation.

In the context of cryptography, Fermat’s Little Theorem provides a mathematical foundation that supports the security mechanisms underlying the digital economy, from banking transactions to confidential communications. As we venture further into an era dominated by quantum computing and advanced AI, the principles of number theory will continue to guide the development of secure, reliable algorithms.

<>

Conclusion

Fermat’s Little Theorem exemplifies the elegance and utility of mathematical concepts derived from number theory, transcending their origins to solve real-world problems. In the ever-evolving field of technology and cybersecurity, the theorem offers a bridge connecting the abstract world of numbers with the concrete requirements of digital security. As we continue to push the boundaries of what’s possible with AI and computing, the insights gained from number theory will undeniably play a pivotal role in shaping the future of technology.

Remember, the applications of number theory in technology exemplify the profound impact that seemingly abstract mathematical concepts can have on our world, underpinning innovations that enhance and secure our digital lives.

Focus Keyphrase: Fermat’s Little Theorem in Cryptography