Exploring Prime Factorization in Number Theory: A Cornerstone of Cybersecurity in AI
Unlocking the Mysteries of Prime Factorization in Number Theory
In the realm of mathematics, Number Theory stands as one of the most intriguing and foundational disciplines, with prime factorization representing a cornerstone concept within this field. This article will explore the mathematical intricacies of prime factorization and illuminate its applications beyond theoretical mathematics, particularly in the areas of cybersecurity within artificial intelligence and cloud solutions, domains where I, David Maiolo, frequently apply advanced mathematical concepts to enhance security measures and optimize processes.
Understanding Prime Factorization
Prime factorization, at its core, involves decomposing a number into a product of prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. The beauty of prime numbers lies in their fundamental role as the “building blocks” of the natural numbers.

The mathematical expression for prime factorization can be represented as:
\[N = p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot p_n^{e_n}\]
where \(N\) is the natural number being factorized, \(p_1, p_2, \ldots, p_n\) are the prime factors of \(N\), and \(e_1, e_2, \ldots, e_n\) are their respective exponents indicating the number of times each prime factor is used in the product.
Applications in Cybersecurity
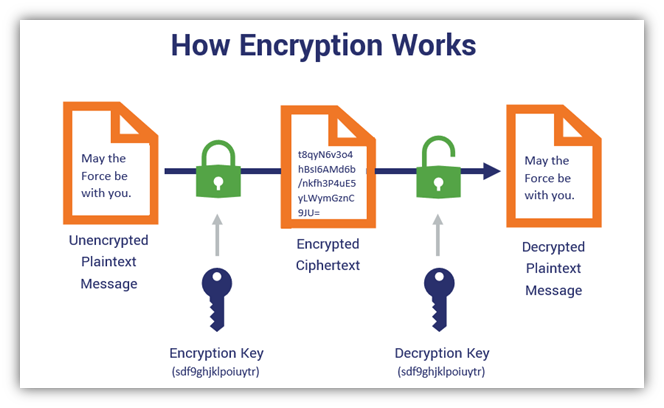
The concept of prime factorization plays a pivotal role in the field of cybersecurity, specifically in the development and application of cryptographic algorithms. Encryption methods, such as RSA (Rivest–Shamir–Adleman), fundamentally rely on the difficulty of factoring large prime numbers. The security of RSA encryption is underpinned by the principle that while it is relatively easy to multiply two large prime numbers, factoring their product back into the original primes is computationally challenging, especially as the size of the numbers increases.
Enhancing AI and Cloud Solutions
In my work through DBGM Consulting, Inc., applying advanced number theory concepts like prime factorization allows for the fortification of AI and cloud-based systems against cyber threats. By integrating robust encryption protocols rooted in number theory, we can ensure the security and integrity of data, a critical concern in both AI development and cloud migrations.
Linking Prime Factorization to Previous Articles
Prime factorization’s relevance extends beyond cybersecurity into the broader mathematical foundations supporting advancements in AI and machine learning, topics discussed in previous articles on my blog. For instance, understanding the role of calculus in neural networks or exploring the future of structured prediction in machine learning necessitates a grounding in basic mathematical principles, including those found in number theory. Prime factorization, with its far-reaching applications, exemplifies the deep interconnectedness of mathematics and modern technological innovations.
Conclusion
The exploration of prime factorization within number theory reveals a world where mathematics serves as the backbone of technological advancements, particularly in securing digital infrastructures. As we push the boundaries of what is possible with artificial intelligence and cloud computing, grounding our innovations in solid mathematical concepts like prime factorization ensures not only their efficiency but also their resilience against evolving cyber threats.
429 for Popular RSA encryption library
In essence, prime factorization embodies the harmony between theoretical mathematics and practical application, a theme that resonates throughout my endeavors in AI, cybersecurity, and cloud solutions at DBGM Consulting, Inc.
Focus Keyphrase:
Prime Factorization in Number Theory









While the article offers a fascinating perspective on prime factorization, I remain cautious about the emphasis on mathematical methods as the ultimate solution for cybersecurity in AI. Given the rapid advancements and the ingenuity of cyber threats, it seems a broader, more flexible approach might be necessary. However, I appreciate the deep dive into number theory’s relevance, a refreshing angle that adds to the ongoing conversation about securing our digital future.
I’m thrilled to share insights into the realm of prime factorization, a subject close to my expertise and passion. Through this article, I hope to unravel the complexities of number theory and its applications, especially in AI and cloud computing’s cybersecurity. My aim is to provide a foundational understanding that encourages further exploration and appreciation of the mathematical underpinnings essential for tomorrow’s technological innovations.